Las aplicaciones de la integral definida son variadas, siendo el cálculo de áreas una de ellas.
Caso 1
Si la función es no negativa en el intervalo , entonces su integral definida sobre el intervalo es el área limitada por su gráfica y el eje OX:
![área bajo la gráfica de f(x) = x^2 en el intervalo [0,2] Recordamos la regla de Barrow y explicamos cómo utilizarla para calcular el área de la región que encierran la gráfica de una función y el eje de abscisas o el área que encierran las gráficas de dos funciones. Con ejemplos y problemas resueltos. Integrales definidas. Bachillerato y universidad. Matemáticas.](https://www.problemasyecuaciones.com/integrales/definida/G0.png)
La representación corresponde a la gráfica de la función
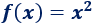
El área que encierra su gráfica con el eje X en el intervalo es la siguiente integral definida:
![calculamos la integral definida de x^2 en el intervalo [0,2], obteniendo 8/3 Recordamos la regla de Barrow y explicamos cómo utilizarla para calcular el área de la región que encierran la gráfica de una función y el eje de abscisas o el área que encierran las gráficas de dos funciones. Con ejemplos y problemas resueltos. Integrales definidas. Bachillerato y universidad. Matemáticas.](https://www.problemasyecuaciones.com/integrales/definida/T3.png)
Caso 2
Si la función es no positiva en el intervalo , entonces su integral definida es el área encerrada entre su gráfica y el eje X, pero con valor negativo:
![área sobre la gráfica de f(x) = -x^2 en el intervalo [0,2] Recordamos la regla de Barrow y explicamos cómo utilizarla para calcular el área de la región que encierran la gráfica de una función y el eje de abscisas o el área que encierran las gráficas de dos funciones. Con ejemplos y problemas resueltos. Integrales definidas. Bachillerato y universidad. Matemáticas.](https://www.problemasyecuaciones.com/integrales/definida/G1.png)
La representación corresponde a la gráfica de la función
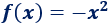
El área que encierra su gráfica con el eje X en el intervalo es el valor absoluto de la integral definida:
![calculamos el valor absoluto de la integral definida de -x^2 en [0,2], obeniendo 8/3 Recordamos la regla de Barrow y explicamos cómo utilizarla para calcular el área de la región que encierran la gráfica de una función y el eje de abscisas o el área que encierran las gráficas de dos funciones. Con ejemplos y problemas resueltos. Integrales definidas. Bachillerato y universidad. Matemáticas.](https://www.problemasyecuaciones.com/integrales/definida/T5.png)
Caso 3.
es negativa y positiva, la región que encierra su gráfica con el eje X está dividida en varias regiones, algunas sobre el eje y otras bajo éste:
![región encerrada entre la gráfica de f(x) = x^2-4x+3 y el eje de abscisas en el intervalo [0,2] Recordamos la regla de Barrow y explicamos cómo utilizarla para calcular el área de la región que encierran la gráfica de una función y el eje de abscisas o el área que encierran las gráficas de dos funciones. Con ejemplos y problemas resueltos. Integrales definidas. Bachillerato y universidad. Matemáticas.](https://www.problemasyecuaciones.com/integrales/definida/G3.png)
La representación corresponde a la gráfica de la función
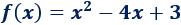
El área que encierra su gráfica con el eje OX en el intervalo esta dividida en dos regiones. Su área es
![el área es la integral definida de f(x) en [0,1] más el valor absoluto de la integral definida de f(x) en [1,2] Recordamos la regla de Barrow y explicamos cómo utilizarla para calcular el área de la región que encierran la gráfica de una función y el eje de abscisas o el área que encierran las gráficas de dos funciones. Con ejemplos y problemas resueltos. Integrales definidas. Bachillerato y universidad. Matemáticas.](https://www.problemasyecuaciones.com/integrales/definida/T8.png)
Tenemos que calcular una integral para cada región porque en la región que está bajo el eje, la integral es negativa.
La primera integral es
![calculamos la integral definida de x^2-4x+3 en [0,1], obteniendo 4/3 Recordamos la regla de Barrow y explicamos cómo utilizarla para calcular el área de la región que encierran la gráfica de una función y el eje de abscisas o el área que encierran las gráficas de dos funciones. Con ejemplos y problemas resueltos. Integrales definidas. Bachillerato y universidad. Matemáticas.](https://www.problemasyecuaciones.com/integrales/definida/T9.png)
La segunda es
![calculamos la integral definida de x^2-4x+3 en [1,2], obteniendo -2/3 Recordamos la regla de Barrow y explicamos cómo utilizarla para calcular el área de la región que encierran la gráfica de una función y el eje de abscisas o el área que encierran las gráficas de dos funciones. Con ejemplos y problemas resueltos. Integrales definidas. Bachillerato y universidad. Matemáticas.](https://www.problemasyecuaciones.com/integrales/definida/T10.png)
Por tanto, el área total de la región es:
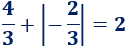 .
.
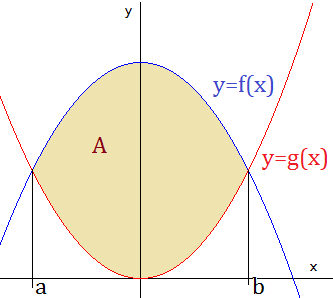

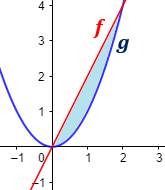
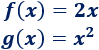
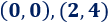
![calculamos la integral definida de 2x-x^2 en [0,2], obteniendo 4/3 Recordamos la regla de Barrow y explicamos cómo utilizarla para calcular el área de la región que encierran la gráfica de una función y el eje de abscisas o el área que encierran las gráficas de dos funciones. Con ejemplos y problemas resueltos. Integrales definidas. Bachillerato y universidad. Matemáticas.](https://www.problemasyecuaciones.com/integrales/definida/T14.png)